MATLAB中计算 是eig（A）。

求矩阵A的特征值。设

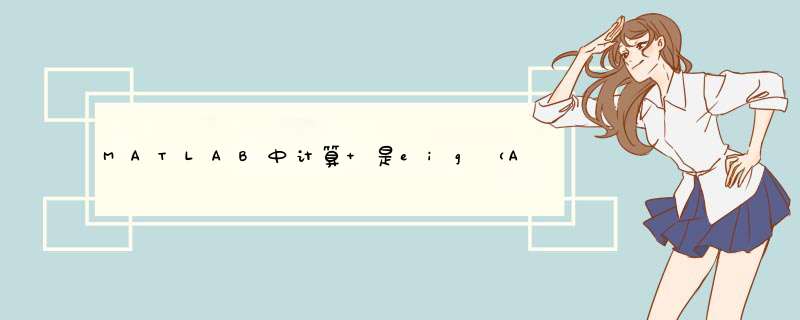
>>A=[1,2,3;40,34,56;-7,19,-87]

d=eig(A)

d=(44189,-12268,-949622)'

特征向量和特征值里面有复数很正常啊，并没有什么问题。

如果你的矩阵是实数矩阵，那么复数特征值一定会以共轭形式成对出现，复数特征向量也是成对的。

[V,D]=eig(A)，D是特征值，V的各列是对应的特征向量，而且V是归一化的矩阵。

不知道你想要的归一化是指什么，里面有很多关于矩阵归一化的提问，你自己可以先查查看。

据我所知eig会分析矩阵的结构选用相应的算法。

如果是eig(A)的形式，取决于A是否是Hermite阵：

如果A是Hermite阵则选用对称QR算法（对小矩阵）和divide and conquer算法（对大矩阵）；

如果A不是Hermite阵则使用非对称QR算法。

如果是eig(A,B)的形式，也取决于对称性：

如果A和B都是Hermite阵且至少有一个半正定，那么应该会利用Cholesky分解归约到普通的对称特征值问题；

如果上述结构不满足，那么会使用QZ算法。

Jacobi算法虽然精度很高，但是速度相对慢一些，所以不作为默认的算法。