概率密度函数f(x)是什么

设：概率分布函数为：F(x)

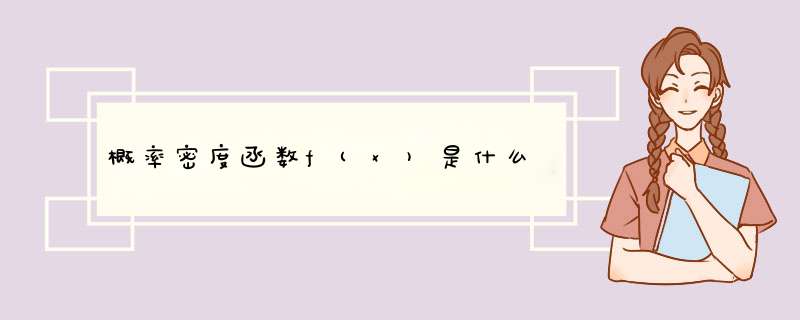
概率密度函数为：f(x)

二者的关系为：f(x) = dF(x)/dx

即：密度函数f 为分布函数 F 的一阶导数。或者分布函数为密度函数的积分。

定义分布函数，是因为在很多情况下，我们并不想知道在某样东西在某个特定的值的概率，顶多想知道在某个范围的概率，于是，就有了分布函数的概念。

而概率密度，如果在x处连续的话。就是分布函数F(x)对x求导，反之，知道概率密度函数，通过负无穷到x的积分，也可以求得分布函数。             

概率密度：

单纯的讲概率密度没有实际的意义，它必须有确定的有界区间为前提。可以把概率密度看成是纵坐标，区间看成是横坐标，概率密度对区间的积分就是面积，而这个面积就是事件在这个区间发生的概率，所有面积的和为1。所以单独分析一个点的概率密度是没有任何意义的，它必须要有区间作为参考和对比。

-概率密度

设随机变量X的密度函数为f(x)=A/x^2，x>100；0，x<=100，系数A为10。

A＝1／（∫［－∞，＋∞］f（x）dx）

＝1／（∫［10，＋∞］a／x＾2dx）

＝1／（－a／x｜［10，＋∞］）

＝1／（a／10）

＝10

扩展资料：

如果随机变量只取得有限个值或无穷能按一定次序一一列出，其值域为一个或若干个有限或无限区间，这样的随机变量属于离散型随机变量。离散型随机变量由随机变量取值范围确定。离散型随机变量的一切可能的取值与对应的概率乘积之和为其数学期望的加权平均。

变量取值只能取离散型的任意有限个相互独立的自然数，如果变量可以在某个区间内取任一实数，则变量的取值可以是连续的。

函数F(x)是定义域A到值域B的一种特殊的映射。

映射F：A——>B，F就是函数三要素中的对应法则，它实际上是一种算法。比如F(x)=2x+1，F就表示x的2倍再加1这样一种算法。

函数的近代定义是给定一个数集A，假设其中的元素为x，对A中的元素x施加对应法则f，记作f（x），得到另一数集B，假设B中的元素为y，则y与x之间的等量关系可以用y=f（x）表示。

函数概念含有三个要素：定义域A、值域B和对应法则f。其中核心是对应法则f，它是函数关系的本质特征。

函数性质：

二次函数是抛物线，但抛物线不一定是二次函数。开口向上或者向下的抛物线才是二次函数。抛物线是轴对称图形。

对称轴为直线x = -b/2a，对称轴与抛物线唯一的交点为抛物线的顶点P。特别地，当b=0时，抛物线的对称轴是y轴（即直线x=0）。

在一维连续型随机变量中，f(x)表示随机变量X的密度函数。

一、含义不同：

fX（x）和fY（y）在“二维连续型随机变量及其密度函数”中出现。

fX（x）是X的边缘密度函数；fY（y）是Y的边缘密度函数。

二、表示不同：

X表示一个变量~x表示一个变量的值，F（X）表示一个函数的话，F（x）表示把X=x代入。

性质

随机变量在不同的条件下由于偶然因素影响，可能取各种不同的值，故其具有不确定性和随机性，但这些取值落在某个范围的概率是一定的，此种变量称为随机变量。随机变量可以是离散型的，也可以是连续型的。

如分析测试中的测定值就是一个以概率取值的随机变量，被测定量的取值可能在某一范围内随机变化，具体取什么值在测定之前是无法确定的，但测定的结果是确定的，多次重复测定所得到的测定值具有统计规律性。

-随机变量