求导sin5x，要详细过程

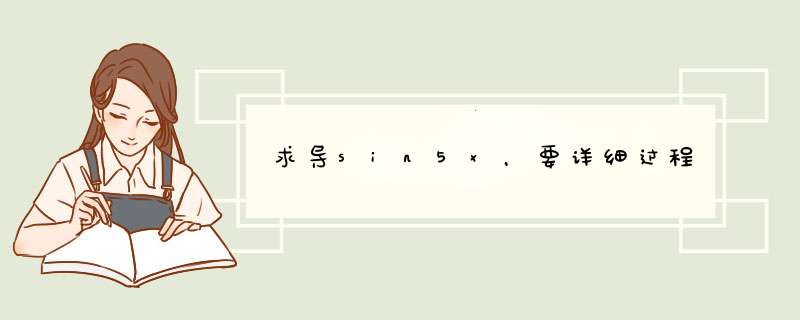
具体回答如下：

不是所有的函数都有导数，一个函数也不一定在所有的点上都有导数。若某函数在某一点导数存在，则称其在这一点可导，否则称为不可导。然而，可导的函数一定连续；不连续的函数一定不可导。

扩展资料：

设函数y=f（x）在点x0的某个邻域内有定义，当自变量x在x0处有增量Δx，（x0+Δx）也在该邻域内时，相应地函数取得增量Δy=f（x0+Δx）-f（x0）。

如果Δy与Δx之比当Δx→0时极限存在，则称函数y=f（x）在点x0处可导，并称这个极限为函数y=f（x）在点x0处的导数。

分解的原则就是按照运算顺序一层一层的去掉,比如y=sin

e^√x,他的最后一步运算时sin,所以先去sin,就设h(x)=sin(x),去掉sin后的最后一步运算是求指数e^√x,所以设g(x)=e^x,接着,去掉e后的最后一步运算是开方√x,所以设f(x)=√x,至此可以把h,g,f复合起来就是原函数了第二题同理

对于y=sin

e^√x,令h(x)=sin(x),g(x)=e^x,f(x)=√x,那么

它们的复合函数h{g[f(x)]}=h[g(√x)]=h(e^√x)=sin

e^√x

对于y=√lntan

x^2,令P(x)=√x,h(x)=ln(x),g(x)=tan(x),f(x)=x^2,那么

它们的复合函数

P{h{g[f(x)]}}=P{h[g(x^2)]}=P{h[tan(x^2)]}=P[lntan(x^2)]=√lntan(x^2)