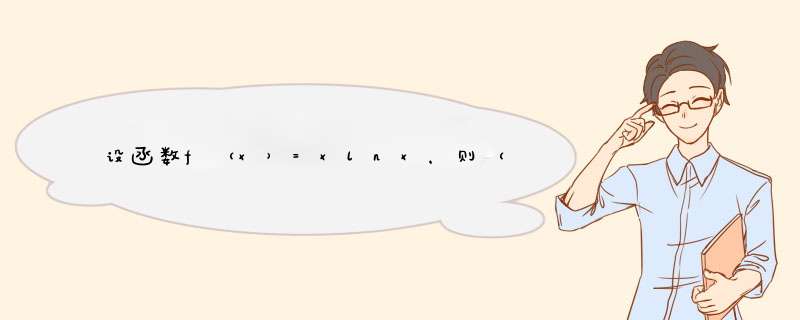
函数的定义域为(0,+∞)
求导函数,可得f′(x)=1+lnx
令f′(x)=1+lnx=0,可得x=
| 1 |
| e |
∴0<x<
| 1 |
| e |
| 1 |
| e |
∴x=
| 1 |
| e |
| 1 |
| e |
故选D.
(1)当a=-1时,f(x)=-x+lnx
f'(x)=-1+1/x
令f'(x)>0,1/x>1,0<x<1
令f'(x)<0,1/x<1,x>1
所以当x=1时,f(x)取得最大值f(1)=-1
(2)f(x)=ax+lnx
f'(x)=a+1/x
令f'(x)>0,1/x>-a,令f'(x)<0,1/x<-a
当a<-1/e(0<-1/a<e)时,f'(x)>0,0<x<-1/a,f'(x)<0,x>-1/a
f(x)在区间(0,e上的最大值为f(-1/a)=-3,-1+ln(-1/a)=-3,a=-e²(符合题意)
当-1/e≤a<0(-1/a>e)时,f'(x)>0,0<x<-1/a,f'(x)<0,x>-1/a
f(x)在区间(0,e上单增,最大值为f(e)=-3,ae+lne=-3,ae=-4,a=-4/e(不符合题意,舍去)
当a≥0时,a+1/x>0,f'(x)>0,
f(x)在区间(0,e上单增,最大值为f(e)=-3,ae+lne=-3,ae=-4,a=-4/e(不符合题意,舍去)
总之,a=-e²
(3)当a=-1时,
|f(x)|=lnx/2+1/2
|-1+1/x|=lnx/2+1/2
当0<x<1时,-1+1/x=lnx/2+1/2,设g(x)=lnx/2-1/x+3/2,g'(x)=1/x+1/x²=(x+1)/x²>0
所以,函数g(x)在区间(0,1)内单增,而g(1)=-ln2-1+3/2=1/2-ln2<0,
所以,g(x)在区间(0,1)内恒小于0,方程|f(x)|=lnx/2+1/2在区间(0,1)内没有实数解
当x≥1时,1-1/x=lnx/2+1/2,设g(x)=lnx/2+1/x-1/2,g'(x)=1/x-1/x²=(x-1)/x²≥0
所以,函数g(x)在区间(1,正无穷)内单增,而g(1)=-ln2+1-1/2=1/2-ln2<0,
g(2e)=1+1/2e-1/2=1/2+1/2e>0,g(1)g(2e)<0
所以方程|f(x)|=lnx/2+1/2在区间(1,2e)有实数解
(2)任意实数x≥0,f(x)>0恒成立
f'(x)=e^x+a
a>=-1时,f(x)=e^x+a>0恒成立,f(x)递增
所以f(x)>=f(0)=1>0恒成立
a<-1时
0<x<ln(-a)时,f'(x)<0,f(x)递减;x>ln(-a)时,f‘(x)>0,f(x)递增
所以f(x)最小值是f(ln(-a))=-a+aln(-a)=(-a)(1-ln(-a))>0
ln(-a)<1 -a<e a>-e
所以综上a>-e
(2)a=-1
y=g(x)-f(x)=e^xlnx-e^x+x
存在实数xo∈[1,e],使曲线C:y=g(X)-f(X)在点x=x0处的切线与y轴垂直
也就是y'(x0)=0
y'(x)=e^xlnx+e^x/x-e^x+1=e^x(lnx+1/x-1)+1
而设h(x)=lnx+1/x-1
h'(x)=1/x-1/x^2=(x-1)/x^2
1<=x<=e h'(x)>0 h(x)递增,h(x)>=h(1)=0
所以e^x(lnx+1/x-1)>0
所以y'(x)=e^x(lnx+1/x-1)+1>=1
所以不会有Y'(x)=0
也就是说不存在符合题意得x0
欢迎分享,转载请注明来源:内存溢出

 微信扫一扫
微信扫一扫
 支付宝扫一扫
支付宝扫一扫
评论列表(0条)