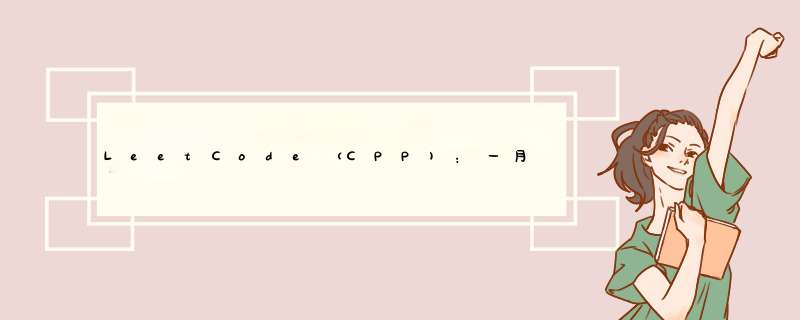
根据题意,当我们在矩阵上填写字符时,会向下填写 r 个字符(行数),然后向右上继续填写 r-2 个字符,最后回到第一行,因此 Z 字形变换的周期 t=r+r-2=2r-2,每个周期会占用矩阵上的 1+r-2=r-1 列。来源:力扣(LeetCode)
在每个周期上,“Z”型变换认为“7”型为一周期,这样每一个周期中第一行和最后一行只有一个元素,其他行都有第一列和“/”型对角线上两个元素,所以枚举时,对每行的周期所包含的元素进行插入ans:所有行都插入第一个元素,非第一行和最后一行在条件(本位值未越界&&本位值加周期未越界)下则可以插入第二个元素。
逐行插入,可以直接返回ans。
class Solution {
public:
string convert(string s, int numRows) {
int n=s.length(),r=numRows;
if(r==1||r>=n){return s;}
string ans;//创建一个数组用于存储新的字符串数据
int T=2*r-2;//周期T中元素个数,就是一个"Z"包含的列数
for(int i=0;i0&&i0&&i 7. 整数反转(mid) 思路:
翻转首先想到了stack,但是负数还要讨论,另外比较占空间;
x%10,可以得到x的最高位数字,下一 *** 作将x/10,删除原数字x的最高位,为提取次高位做铺垫;
提取到高位数字后,把它们依次放到地位,循环执行(原先 i 位)*10+(原先 i-1 位);
代码很清楚。
class Solution{
public:
int reverse(int x){
int rev=0;
while(x!=0)
{
if(revINT_MAX/10){return 0;}//越界返回0
int digit=x%10;//提取x的最高位数字
x/=10;//从高到低的下一位
rev=rev*10+digit;//x的最高位数字作为rev的最低位数字
}
return rev;
}
}; 8.字符串转换整数(atoi)(mid) 思路:
不如说是提取字符串中的数字(含负数)
本题使用了自动机DFS,也是我第一次见,我的理解就是把每个可能的情况列举出来。
class Automaton{//创建Automaton类
string state="start";
unordered_map> table={//使用map容器,前面是关键字,后面是对应的值
{"start",{"start","signed","in_number","end"}},
{"signed",{"end","end","in_number","end"}},
{"in_number",{"end","end","in_number","end"}},
{"end",{"end","end","end","end"}}
};
int get_col(char c){
if(isspace(c)) return 0;//isspace,判断c是否为空
if(c=='+'||c=='-') return 1;
if(isdigit(c)) return 2;//isdigit,判断是否为数字
return 3;
}//0123分别用于找到table中vector容器内下标字符串
public:
int sign = 1;
long long ans =0;
void get(char c){
state=table[state][get_col(c)];
if(state=="in_number"){
ans= ans*10+c-'0';//-'0',是把'2'转化为2,'0'为ASCII值,字符数字转化为纯数字必须-'0'
ans= sign==1? min(ans,(long long)INT_MAX) : min(ans,-(long long)INT_MIN);//判断是否超出范围?
}
else if(state=="signed"){
sign=c=='+'?1:-1;
}
}
};
class Solution {
public:
int myAtoi(string s) {
Automaton automaton;//创建自动机对象,DFA,确定自动机
for(char c:s)//遍历s中的字符,令其为c
automaton.get(c);
return automaton.sign*automaton.ans;
}
}; 9. 回文数(easy)
class Solution {
public:
bool isPalindrome(int x) {
// 特殊情况:
// 如上所述,当 x < 0 时,x 不是回文数。
// 同样地,如果数字的最后一位是 0,为了使该数字为回文,
// 则其第一位数字也应该是 0
// 只有 0 满足这一属性
if (x < 0 || (x % 10 == 0 && x != 0)) {
return false;
}
int reNum = 0;
while (x > reNum) {
reNum = reNum * 10 + x % 10;
x /= 10;
}
// 当数字长度为奇数时,我们可以通过 reNum/10 去除处于中位的数字。
// 例如,当输入为 12321 时,在 while 循环的末尾我们可以得到 x = 12,reNum = 123,
// 由于处于中位的数字不影响回文(它总是与自己相等),所以我们可以简单地将其去除。
return x == reNum || x == reNum / 10;//只要有一个是true,返回true
}
};10. 正则表达式(hard)
dp五部曲:
设主串s的长度为m,设模式串p的长度为n;其中s只有小写字母,p有字母/./*
1.状态定义:dp[i][j]为考虑s[0,i-1]与p[0,j-1]是否能匹配上,能匹配上就为true
2.状态转移:若要求dp[i][j]就必须考虑到s[i-1]与p[j-1]
2.1 当p[j-1]不是'*'时
2.1.1 若s[i-1]==p[j-1]时,即p[j-1]为'a'-'z'且与s[i-1]相等,看dp[i-1][j-1]
2.1.2 p[j-1] == '.'时,直接将'.'变成s[i-1],看dp[i-1][j-1]
注意:这里的'.'是匹配一个字符,而不是一连串,如"a.b"->"axb"
2.2 当p[j-1]是'*'时,主要看p[j-2]做判断
2.2.1 p[j-2]为'a'-'z'并且p[j-2]==s[i-1],那么此时s继续往前看,p暂时不动
即:看dp[i-1][j]
2.2.2 p[j-2]为'.',那么".*"可以变为"....."可以匹配s[i-1]前面的任何字符(万能串)
因此,直接看dp[i-1][j](或者直接返回true)
2.2.3 剩下的就是p[j-2]为'a'-'z'且p[j-2]!=s[i-1],那么此时p的"x*"作废,看dp[i][j-2]
这里:2.1.1与2.2.2可以看成一种情形:即s与p均前移一位
2.2.1与2.2.2可以看成一种情形:即p不动s前移一位
3.初始化:
3.1 空的s
3.1.1 空的p,空的s可以匹配空的p,因此dp[0][0]=true
3.1.2 非空的p,空的s可能可以匹配非空的p,例如"a*",因此需要经过转移计算
3.2 空的p
3.2.1 空的s,同3.1.1
3.2.2 非空的s,空的p不可能匹配非空的s,因此dp[i][0]=false,i∈[1,m]
3.3 非空的s与非空的p:需要经过转移计算
其中:3.1.1与3.2.2可以合并为dp[i][0]=i==0
4.遍历顺序:显然是正序遍历
5.返回形式:返回dp[m][n]就是考虑s[0,m-1]与p[0,n-1]是否能匹配上
受代码随想录carl的启发:
我个人觉得比较好理解的五部曲是这样:
1.明白数组dp[i]或dp[i][j]表示了什么含义;
2.dp数组的初始化,可能是dp[0],也可能是首行和首列(不同路径问题);
3.状态转移方程,dp[i][j]是怎么样与前面的状态dp[i-1][j-1]ordp[i-1][j]....相联系的,明白了这个就解决了一大半问题;
4.遍历顺序,从前往后还是从后往前,先干什么再干什么
5.输出结果,即最终的结果保存在哪里,dp[i-1][j-1]?
带入这道题中:
1.dp[i][j] 的含义:s 的前 i 个字符与 p 的前 j 个字符是否能够匹配,匹配为true,不能匹配为false
2.初始化: dp[0][0] = true; 这里还是比较绕的,没有具体的含义,就是没有任何字符就是匹配的,空==空。
3.状态转移方程:几个最基本的逻辑如下
(1)字母对字母,相同或不同;(2)字母对“.",则任意匹配,总是true;(3)字母对” * ",可以浪费也可以匹配多个前面的那一个元素
那么相应的状态转移就会是:(来自力扣)
(1)最简单的,如果此时的s[i]和p[j]相同,则比较前面一个字符,否则匹配不成功;
(2)" . "可以匹配一个任意元素:f[i][j]=f[i-1][j-1]
(3)" * "最复杂,可以对 p 的第 j−1 个字符匹配任意自然数次。在匹配 0 次的情况下,我们有
在匹配 1,2,3, ⋯ 次的情况下,类似地我们有:
最终有:
所以最终的状态转移方程:
其中matches(x,y) 判断两个字符是否匹配的辅助函数。只有当 y 是 . 或者 x 和 y 本身相同时,这两个字符才会匹配。
需要注意的是,运算是bool类型的,所以code采用 |= 的形式,两个量都不为true时即匹配失败。
作者:LeetCode-Solution
链接:https://leetcode-cn.com/problems/regular-expression-matching/solution/zheng-ze-biao-da-shi-pi-pei-by-leetcode-solution/
来源:力扣(LeetCode)
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。
4.遍历顺序:从后往前;从p中找字符与s对比,先遍历s,在循环中再遍历p;
5.输出的结果放在dp[m][n],结尾处,如果dp[m][n]为true,即代表s 的前 m 个字符与 p 的前 n 个字符能够匹配
class Solution {
public:
bool isMatch(string s, string p) {
int m = s.size();
int n = p.size();
//用来判断是否在这一位置匹配上
auto matches = [&](int i, int j)
{
if (i == 0) {//s中没有元素
return false;
}
if (p[j - 1] == '.') {
return true;
}
return s[i - 1] == p[j - 1];
};
vector> dp(m + 1, vector(n + 1));
dp[0][0] = true;//初始化
for (int i = 0; i <= m; ++i) {//遍历
for (int j = 1; j <= n; ++j) {
if (p[j - 1] == '*') {
dp[i][j] |= dp[i][j - 2];
if (matches(i, j - 1)) {
dp[i][j] |= dp[i - 1][j];//状态转移方程
}
}
else {//不为*
if (matches(i, j)) {
dp[i][j] |= dp[i - 1][j - 1];//状态转移方程
}
}
}
}
return dp[m][n];//返回某个dp量
}
}; 欢迎分享,转载请注明来源:内存溢出

 微信扫一扫
微信扫一扫
 支付宝扫一扫
支付宝扫一扫
评论列表(0条)