用MATLAB+计算1-1000立方和的程序？

以下是一个使用MATLAB编写的程序，可以计算1-1000的立方和：

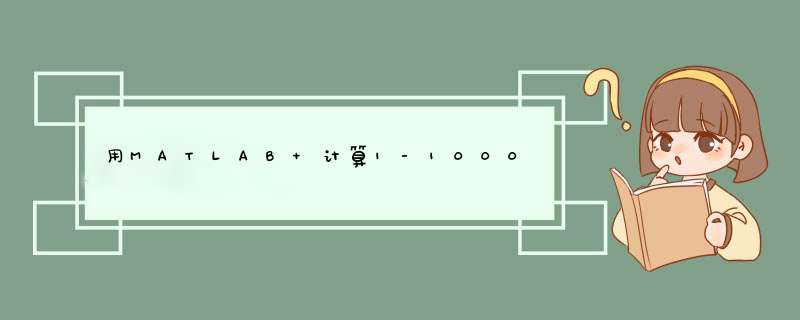
n = 1000 % 设置上限

% 计算立方和

sum = 0

for i = 1:n

sum = sum + i^3

end

% 输出结果

disp(sum)

首先定义了上限值n为1000，然后使用for循环来计算1到n的立方和。具体地，在每次循环中，将当前数字的立方加入到 sum 变量中。

最后，使用disp()函数将计算结果输出到命令窗口中。

在计算大量数据时，程序可能需要较长的运行时间和大量的内存空间。如果需要对更大范围的数进行求和，可能需要对代码进行优化或采用更高效的算法。

在聚类分析中，K-均值聚类算法(k-means

algorithm)是无监督分类中的一种基本方法，其也称为C-均值算法，其基本思想是:通过迭代的方法，逐次更新各聚类中心的值，直至得到最好的聚类结果。

假设要把样本集分为c个类别，算法如下:

(1)适当选择c个类的初始中心

(2)在第k次迭代中，对任意一个样本，求其到c个中心的距离，将该样本归到距离最短的中心所在的类，

(3)利用均值等方法更新该类的中心值

(4)对于所有的c个聚类中心，如果利用(2)(3)的迭代法更新后，值保持不变，则迭代结束，否则继续迭代。

下面介绍作者编写的一个分两类的程序，可以把其作为函数调用。

%%

function

[samp1,samp2]=kmeans(samp)

作为调用函数时去掉注释符

samp=[11.1506

6.7222

2.3139

5.9018

11.0827

5.7459

13.2174

13.8243

4.8005

0.9370

12.3576]

%样本集

[l0

l]=size(samp)

%%利用均值把样本分为两类，再将每类的均值作为聚类中心

th0=mean(samp)n1=0n2=0c1=0.0c1=double(c1)c2=c1for

i=1:lif

samp(i)<th0

c1=c1+samp(i)n1=n1+1elsec2=c2+samp(i)n2=n2+1endendc1=c1/n1c2=c2/n2

%初始聚类中心t=0cl1=c1cl2=c2

c11=c1c22=c2

%聚类中心while

t==0samp1=zeros(1,l)

samp2=samp1n1=1n2=1for

i=1:lif

abs(samp(i)-c11)<abs(samp(i)-c22)

samp1(n1)=samp(i)

cl1=cl1+samp(i)n1=n1+1

c11=cl1/n1elsesamp2(n2)=samp(i)

cl2=cl2+samp(i)n2=n2+1

c22=cl2/n2endendif

c11==c1

&&

c22==c2t=1endcl1=c11cl2=c22

c1=c11c2=c22

end

%samp1,samp2为聚类的结果。

初始中心值这里采用均值的办法，也可以根据问题的性质，用经验的方法来确定，或者将样本集随机分成c类，计算每类的均值。

k-均值算法需要事先知道分类的数量，这是其不足之处。

---