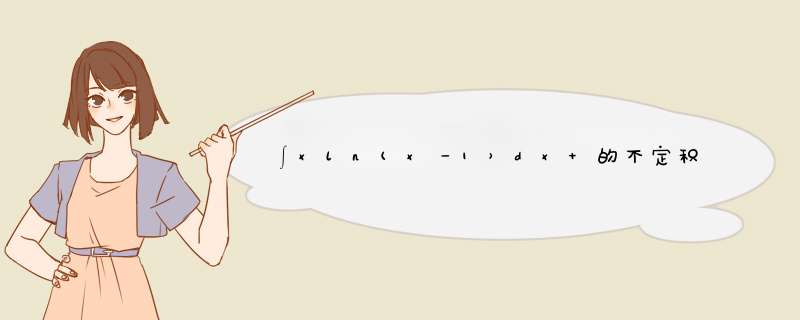
∫xln(x-1)dx=x^2/2* ln(x-1)-x^2/4-x/2-ln(x-1)/2+C。
解答过程如下:利用分部积分法可求得
∫xln(x-1)dx
=1/2x²ln(1+x)-1/2[x²/2-x+ln(1+x)]+C∫x ln(x-1)dx=x^2/2* ln(x-1)-∫x^2/2ln(x-1)'dx
=x^2/2* ln(x-1)-∫x^2/2(x-1)dx
=x^2/2* ln(x-1)-∫(x^2-x)/2(x-1)dx-∫x/2(x-1)dx
=x^2/2* ln(x-1)-∫x/2dx-∫x/2(x-1)dx
=x^2/2* ln(x-1)-x^2/4-∫x/2(x-1)dx
=x^2/2* ln(x-1)-x^2/4-∫(x-1)/2(x-1)dx-∫1/2(x-1)dx
=x^2/2* ln(x-1)-x^2/4-∫1/2dx-∫1/2(x-1)d(x-1)
=x^2/2* ln(x-1)-x^2/4-x/2-∫1/2(x-1)d(x-1)
=x^2/2* ln(x-1)-x^2/4-x/2-ln(x-1)/2+C
扩展资料
分部积分法两个原则
1、相对来说,谁易凑到微分后面,就凑谁;
2、交换位置之后的积分容易求出。
经验顺序:对,反,幂,三,指
谁在后面就把谁凑到微分的后面去,比如,如果被积函数有指数函数,就优先把指数凑到微分的后面去,如果没有就考虑把三角函数凑到后面去,在考虑幂函数。
当然,对数函数和反三角函数,这两个函数比较难惹,你千万不要动它。需要注意的是经验顺序不是绝对的,而是一个笼统的顺序,掌握两大原则更重要。
过程如下:
∫xlnxdx
=(1/2)∫lnxd(x²)
=(1/2)x²lnx-(1/2)∫x²*(1/x)dx
=(1/2)x²lnx-(1/2)∫xdx
=(1/2)x²lnx-(1/4)x²+C
扩展资料:
对于一个函数f,如果在闭区间[a,b]上,无论怎样进行取样分割,只要它的子区间长度最大值足够小,函数f的黎曼和都会趋向于一个确定的值S,那么f在闭区间[a,b]上的黎曼积分存在,并且定义为黎曼和的极限S。
如果一个函数f在某个区间上黎曼可积,并且在此区间上大于等于零。那么它在这个区间上的积分也大于等于零。如果f勒贝格可积并且几乎总是大于等于零,那么它的勒贝格积分也大于等于零。
作为推论,如果两个l上的可积函数f和g相比,f(几乎)总是小于等于g,那么f的(勒贝格)积分也小于等于g的(勒贝格)积分。
欢迎分享,转载请注明来源:内存溢出

 微信扫一扫
微信扫一扫
 支付宝扫一扫
支付宝扫一扫
评论列表(0条)