已知函数f(x)=x^2+alnx.

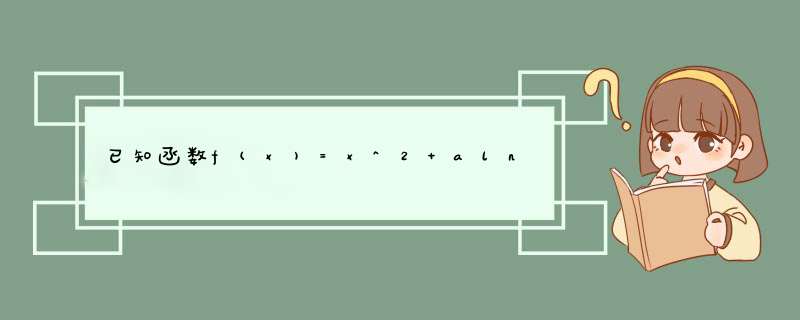
定义域是x>0;

1f(x)=x^2-lnx

f'(x)=2x-1/x

解f'(x)<0，得：0<x<√2/2,这个是单减区间；

单增区间是：[√2/2,正无穷)

f(x)在√2/2取极小值为：1/2-ln(√2/2)

2f'(x)=2x-a/x

当a<=0时，f'(x)>0,成立；

当a>0时，

解f'(x)<0，得：0<x<√(a/2),这个是单减区间；

所以，解√(a/2)<=1得：0<a<=2

综上：a<=2

∫1/(sinx+cosx) dx

=∫1/[√2·(sinxcosπ/4+sinπ/4·cosx)]dx

=∫1/[√2·sin(x+π/4)] dx

=√2/2 ∫csc(x+π/4) d(x+π/4)

=√2/2 ln|csc(x+π/4)-cot(x+π/4)|+C

一个函数，可以存在不定积分，而不存在定积分，也可以存在定积分，而没有不定积分。

扩展资料：

求函数f(x)的不定积分，就是要求出f(x)的所有的原函数，由原函数的性质可知，只要求出函数f(x)的一个原函数，再加上任意的常数C就得到函数f(x)的不定积分。

设G(x)是f(x)的另一个原函数，即∀x∈I，G'(x)=f(x)。于是[G(x)-F(x)]'=G'(x)-F'(x)=f(x)-f(x)=0。

由于在一个区间上导数恒为零的函数必为常数，所以G(x)-F(x)=C’(C‘为某个常数)。

如果上限x在区间[a,b]上任意变动，则对于每一个取定的x值，定积分有一个对应值，所以它在[a,b]上定义了一个函数，这就是积分变限函数。

若函数f(x)在区间[a,b]上连续，则积分变上限函数就是f(x)在[a,b]上的一个原函数。

——不定积分

①充分性

当a=1时，f（x）=x-1-lnx，f'（x）=1-1 x =x-1 x∴当x＞1时，f'（x）＞0，所以函数f（x）在（1，+∞）上是增函数，

当0＜x＜1时，f'（x）＜0，所以函数f（x）在（0，1）上是减函数，

∴f（x）≥f（1）=0

②必要性

f'（x）=1-a x =x-a x ，其中x＞0

（i）当a≤0时，f'（x）＞0恒成立，所以函数f（x）在（0，+∞）上是增函数

而f（1）=0，所以当x∈（0，1）时，f（x）＜0，与f（x）≥0恒成立相矛盾

∴a≤0不满足题意．

（ii）当a＞0时，∵x＞a时，f'（x）＞0，所以函数f（x）在（a，+∞）上是增函数；

0＜x＜a时，f'（x）＜0，所以函数f（x）在（0，a）上是减函数；

∴f（x）≥f（a）=a-a-alna

∵f（1）=0，所以当a≠1时，f（a）＜f（1）=0，此时与f（x）≥0恒成立相矛盾

∴a=1

综上所述，f（x）≥0恒成立的充要条件是a=1；

在x=1有最大值就是指，这个函数求导后的值在带点处等于0，

f'(x)=1-(a/x)-(b/x^2)

f'(1)=1-a-b=0

a+b=1

还有什么问题吗》可以追问