（sinx）²x的不定积分

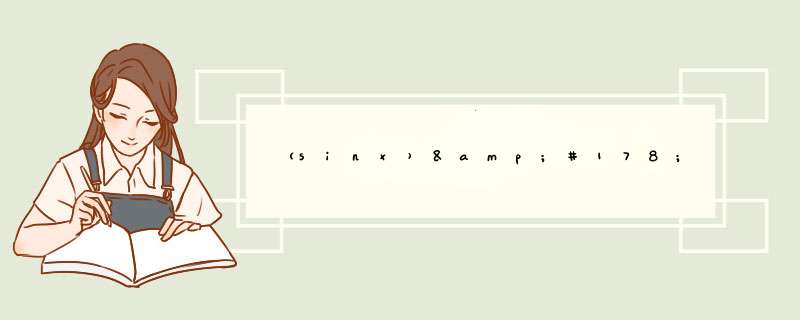
sinx/x的不定积分：

∫sinxdx/x

=-∫dcosx/x=-cosx/x+∫cosxd(1/x)

=-cosx/x+∫dsinx/x^2

=-cosx/x+sinx/x^2+2∫sinxdx/x^3

=-cosx/x+sinx/x^2-2cosx/x^3+2∫cosxd(1/x^3)

=-cosx/x+sinx/x^2-2cosx/x^3+6sinx/x^4+24∫sinxdx/x^5

=-cosx/x+sinx/x^2-2cosx/x^3+6sinx/x^4-24cosx/x^5++(2n-1)!(-1)^(2n-1) cosx/x^(2n-1)+(2n)!sinx/x^(2n)

这个极限好求，不定积分却是已经有定论的：不能用初等函数表示，用初等方法积不出来的。sinx/x的不定积分要用一种叫椭圆积分的方法表示的。

比如∫[0,+∞)e^(-x^2)dx=√π/2，此处的积分值就是用二重积分和极限夹逼的方法得出的，而且只能算出(-∞,+∞)或是(0,+∞)上的值，其他的值只能用数值方法算出近似值。

扩展资料：

把函数f(x)的所有原函数F(x)+ C(其中，C为任意常数）叫做函数f(x)的不定积分，又叫做函数f(x)的反导数，记作∫f(x)dx或者∫f（高等微积分中常省去dx），即∫f(x)dx=F(x)+C。

其中∫叫做积分号，f(x)叫做被积函数，x叫做积分变量，f(x)dx叫做被积式，C叫做积分常数或积分常量，求已知函数的不定积分的过程叫做对这个函数进行不定积分。

由定义可知：

求函数f(x)的不定积分，就是要求出f(x)的所有的原函数，由原函数的性质可知，只要求出函数f(x)的一个原函数，再加上任意的常数C就得到函数f(x)的不定积分。

-不定积分

∫lntanx/(sinxcosx)dx

分子分母同除以cos²x

=∫sec²xlntanx/tanx dx

=∫lntanx/tanx d(tanx)

=∫lntanxd(lntanx)

=(1/2)ln²(tanx)+C

求函数f(x)的不定积分，就是要求出f(x)的所有的原函数，由原函数的性质可知，只要求出函数f(x)的一个原函数，再加上任意的常数C就得到函数f(x)的不定积分。

扩展资料：

由于在一个区间上导数恒为零的函数必为常数，所以G(x)-F(x)=C’(C‘为某个常数)。

这表明G(x)与F(x)只差一个常数因此,当C为任意常数时，表达式F(x)+C就可以表示f(x)的任意一个原函数。也就是说f(x)的全体原函数所组成的集合就是函数族{F(x)+C|-∞<C<+∞}。

虽然很多函数都可通过如上的各种手段计算其不定积分，但这并不意味着所有的函数的原函数都可以表示成初等函数的有限次复合，原函数不可以表示成初等函数的有限次复合的函数称为不可积函数。

——不定积分

解:原式=(1/2)∫[(x^2+1-1)/√(1+x^2)]d(x^2)

=(1/2)∫[(x^2+1)/√(1+x^2)]d(x^2)

-(1/2)∫[1/√(1+x^2)]d(x^2)

=(1/2)∫{[(√(1+x^2))^2]/√(1+x^2)}d(x^2)

-(1/2)∫[1/√(1+x^2)]d(x^2)

=(1/2)∫√(1+x^2)d(x^2)

-(1/2)∫[1/√(1+x^2)]d(x^2)

=(1/2)∫√(1+x^2)d(1+x^2)

-(1/2)∫[1/√(1+x^2)]d(1+x^2)

狄利克雷函数的公式定义：实数域上的狄利克雷（Dirichlet）函数表示为：（k，j为整数）也可以简单地表示分段函数的形式D(x)=0（x是无理数）或1（x是有理数）。

狄利克雷函数是一个定义容在实数范围上、值域不连续的函数。狄利克雷函数的图像以Y轴为对称轴,是一个偶函数,它处处不连续,处处极限不存在,不可黎曼积分。

f'(x)=2x

原函数的定义

F'(x)=f(x)

F(x)是f(x)的原函数

则f(x)是2x的一个原函数

因为(x^2)'=2x

所以f(x)=2x+C

根据定义微分与积分实际上是互为逆运算，即微分是已知原函数然后求导，

求不定积分是已知导数求原函数。然而求一个函数的导函数往往很好求，

求导甚至不需要知道具体的表达式（如隐函数的求导），但反过来

求不定积分，就不是那么容易了。所以一些基本函数与其导函数的转化关系

一定要熟，当已知导函数，立刻想到其原函数，问题便会迎刃而解。所以

导数与原函数的对应关系（即所谓的常用导数表或积分表），一定要熟。

根据原始的不定积分定义，求不定积分，就得熟知积分表，抛开它就

无法下手。

然而求导是可以根据定义来做的，比如已知lim{f(x+dx)-f(x)/dx}=2x,dx趋向0，根据导数定义，这句话就是要告诉我们f'(x)=2x,求它的原函数就得根据

简单的导数与其原函数的对应关系来求。因为f'(x)=(x^2+C)'=2x,所以

其原函数为f(x)=x^2+C